Array
2022. 12. 22. 15:51ㆍCS/자료구조
Array
Array : <index, value> 쌍의 집합
Data Structure
- 각각의 인덱스에는 그 인덱스와 연관된 값이 있다.
표현법
- 연속된(consecutive) 메모리로 구현
- 수학적 표현으로, 대응(correspondence) 또는 매핑(mapping)
List in Python

- 리스트 자체를 가르키는 메모리 주소가 있다.
- 각각의 인덱스에 대응하는 값은 그 다음부터 등장
class Array:
def __init__(self, len=10):
self.len = len
self.data = [0] * len
def __str__(self):
return f"{self.data}"
def __len__(self):
return len(self.data)
def __setitem__(self, id, elem):
self.data[id] = elem
def __getitem__(self, id):
return self.data[id]
if __name__ == "__main__":
# Array객체 instance 를 하나 생성한다
# 기본크기는 10 개이다
arr = Array(5)
for i in range(len(arr)):
arr[i] = i
print(arr)
index = 3
print(f"arr[{index}] = {arr[index]}")
for i in arr:
print(id(i), i)
print(sum(arr))Ordered List
Linear List or Ordered List
- (Item1, Item2, Item3, ...)
- (Sunday, Monday, Tuesday, Wednesday, Thursday, Friday, Saturday)
- etc
class OrderedList():
def __init__(self):
self.elems = []
def __repr__(self):
return str(self.elems)
def __len__(self):
return len(self.elems)
def __getitem__(self, index):
return self.elems[index]
def __str__(self):
return str(self.elems)
def is_empty(self):
return not bool(self.elems)
def add(self, elem):
if not self.elems:
self.elems.append(elem)
return
cur = 0
while cur < len(self) and self[cur] <= elem:
# 삽입할 위치가 배열의 범위를 벗어나지 않고
# 현재 위치의 값이 elem 보다 작으면
cur += 1 #인덱스를 증가
self.elems.insert(cur, elem) #반복문이 끝난 뒤 elem 삽입
def remove(self, elem):
self.elems.remove(elem)
def search(self, elem): #elem이 배열 안에 있는지 여부
cur = 0
while cur < len(self) and self[cur] != elem:
cur += 1
return True if cur <= len(self) else False
def index(self, num): #num값의 위치 반환
cur = 0
if num in self.elems:
while cur < len(self) and self[cur] != num:
cur += 1
return cur
else:
return NoneSparse Matrix
- 일반적인 행렬의 표현은 2차원 배열로 표현한다.
- a[MAX_ROWS][MAX_COLS]
- a[m][n] - Sparse Matrix
- 많은 0으로 구성된 행렬
- 2차원 배열로 Sparse Matrix를 구현하면 낭비하는 메모리가 많다. - Representation
- <row, col, value> 형태로 element를 표현
- 각 행 마다 <row, col, value> 저장
- 각 행에 대해, 열은 오름차순
- 행 번호, 열 번호, 0이 아닌 element 값 저장
class Term:
def __init__(self, row=0, col=0, value=0):
self.row = row
self.col = col
self.value = value
def __str__(self):
return f"{self.row, self.col, self.value}"
def __repr__(self):
return str(self)
class MatrixSparse:
def __init__(self, rows=0, cols=0, size=0, sparse=[]):
self.rows = rows
self.cols = cols
self.size = size
self.sparse = sparse
def build_matrix_sparse(self, mat):
self.rows = len(mat)
self.cols = len(mat[0])
self.sparse = [ #v가 0이 아닐 때,
Term(r, c, v) #Term을 생성
for r, row in enumerate(mat) #r은 mat의 첫 번째 index, row는 그 index의 값(배열)
for c, v in enumerate(row) #받은 배열을 가지고 c는 column, v는 value
if v != 0
]
self.size = len(self.sparse)Transposing Matrix
def transpose(self):
if self.sparse is None:
return
sparse = [Term() for _ in range(self.size)]
idx = 0
for i in range(self.cols):
for e in self.sparse:
if e.col != i:
continue
sparse[idx].row = e.col
sparse[idx].col = e.row
sparse[idx].value = e.value
idx += 1
self.sparse = sparse
return MatrixSparse(
rows=self.cols,
cols=self.rows,
size=self.size,
sparse=sparse,
)Fast Transpose Algorithm


def transpose_fast(self):
rowsize = [0] * self.cols
for i in range(self.cols):
for e in self.sparse:
if e.col == i:
rowsize[i] += 1
print(f"Row size = {rowsize}")
rowstart = [0] * self.cols
for i in range(len(rowstart) - 1):
rowstart[i + 1] = rowsize[i] + rowstart[i]
print(f"Row start = {rowstart}")
if self.sparse is None:
return
sparse = [Term() for _ in range(self.size)]
for e in self.sparse:
sparse[rowstart[e.col]].row = e.col
sparse[rowstart[e.col]].col = e.row
sparse[rowstart[e.col]].value = e.value
rowstart[e.col] += 1
self.sparse = sparse
return sparserowsize 배열을 만들어서 각 index마다 column값이 존재하면 rowsize[i] += 1
rowstart 배열은 각 인덱스마다 시작점을 저장함.
sparse 배열에 Term()을 size만큼 초기화 해주고
rowstart[e.col]의 값으로 sparse 배열에 접근해서 e.col과 row를 각각 반대로 저장해줌.
그리고 rowstart[e.col] += 1
Polynomial
class Polynomial:
def __init__(self, degree):
self.degree = degree
self.coef = [0] * (self.degree + 1)
def get_lead_exp(self): # 최고차항 찾기
i = len(self.coef) - 1
while i >= 0 and self.coef[i] == 0:
i -= 1
if i < 0:
raise Exception("Failed to get_lead_exp.")
return i
def evaluate(self, x):
return sum(
(coef * (x ** exp) for exp, coef in enumerate(self.coef) if coef != 0)
#exp = 인덱스, coef = 값
)
def get_coef(self, exp): # 계수 찾기
return self.coef[exp]
def is_zero(self):
return not any(self.coef)
def zero(self):
for i in range(len(self.coef)):
self.coef[i] = 0
def attach(self, coef, exp):
self.coef[exp] = coef
return self
def remove(self, exp):
self.coef[exp] = 0
def __str__(self):
ret = ""
for coef, exp in [
(self.coef[i], i) for i in range(self.degree + 1) if self.coef[i] != 0][::-1]:
ret += f"({coef})x^{exp} + "
return f"{ret}\b\b"
def __add__(self, other):
poly = Polynomial(max(self.degree, other.degree))
while not self.is_zero() or not other.is_zero():
exp_01 = self.get_lead_exp()
exp_02 = other.get_lead_exp()
if exp_01 > exp_02:
poly.attach(self.get_coef(exp_01), exp_01)
self.remove(exp_01)
elif exp_01 < exp_02:
poly.attach(other.get_coef(exp_02), exp_02)
other.remove(exp_02)
else:
coef = self.get_coef(exp_01) + other.get_coef(exp_02)
exp = exp_01
poly.attach(coef, exp)
self.remove(exp_01)
other.remove(exp_02)
return poly
def __mul__(self, other):
poly = Polynomial(self.degree + other.degree)
temp = Polynomial(self.degree + other.degree)
for coef, exp in [
(self.coef[i] * other.coef[j], i + j)
for i in range(self.degree + 1) if self.coef[i] != 0
for j in range(other.degree + 1) if other.coef[j] != 0
][::-1]:
if poly.get_coef(exp) != 0: #같은 차수 덧셈
temp.attach(coef, exp)
poly = temp + poly
else:
poly.attach(coef, exp)
return poly이 방법은 최고차수만큼 메모리를 할당하기 때문에 계산이 쉽다는 장점이 있으나, 메모리 낭비가 심함.
메모리 관리를 위해 Term을 사용
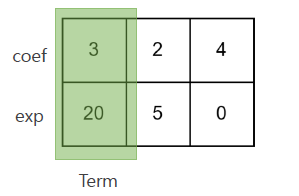
class Term:
def __init__(self, coef =0, exp =0):
self.coef = coef
self.exp = exp
def __repr__(self):
return str(self)
def __str__(self):
return f"{self.coef, self.exp}"
class Polynomial:
def __init__(self):
self.bgn = 0
self.end = 0
self.terms = []
def attach(self, coef=0, exp=0):
self.terms.append(Term(coef, exp))
return self
def evaluate(self, x):
return sum((i.coef * (x**i.exp) for i in self.terms))
def find_term(self, exp):
i = 0
while i < len(self.terms) and self.terms[i].exp != exp:
i += 1
return self.terms[i] if i < len(self.terms) else None
def __str__(self):
ret = ""
terms = sorted(self.terms, key=lambda x: x.exp, reverse=True)
for i in terms:
ret += f"({i.coef})x^{i.exp} + "
return f"{ret}\b\b\b"
def __add__(self, other):
poly = Polynomial()
terms_a = self.terms
terms_b = other.terms
pos_a, pos_b = 0, 0
while pos_a < len(terms_a) and pos_b < len(terms_b):
term_a, term_b = terms_a[pos_a], terms_b[pos_b]
if term_a.exp > term_b.exp:
poly.attach(term_a.coef, term_a.exp)
pos_a += 1
elif term_a.exp < term_b.exp:
poly.attach(term_b.coef, term_b.exp)
pos_b += 1
else:
coef = term_a.coef + term_b.coef
if coef != 0:
poly.attach(coef, term_a.exp)
pos_a += 1
pos_b += 1
while pos_a < len(terms_a):
term = terms_a[pos_a]
poly.attach(term.coef, term.exp)
pos_a += 1
while pos_b < len(terms_b):
term = terms_b[pos_b]
poly.attach(term.coef, term.exp)
pos_b += 1
return poly
def __mul__(self, other): #과제
poly = Polynomial()
for i in self.terms:
for j in other.terms:
exp = i.exp + j.exp
coef = i.coef * j.coef
term = poly.find_term(exp)
if term is None:
poly.attach(coef, exp)
else:
term.coef += coef
return poly